la circunferencia

baricentro

triangulo

En GEOMETRIA , el baricentro o centroide de una superficie contenida en una figura geometrica plana, es un punto tal, que cualquier recta que pasa por él, divide a dicha superficie en dos partes de igual momento respecto a dicha recta.

EL TRIANGULO

Un triángulo, engeometria, es un poligono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vertices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.

Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 lados y 3 vértices.

El Teorema de Pitágoras establece que en untriangulo rctangulo , el cuadrado de la longitud de la hipotenusa(el lado de mayor longitud del triángulo rectángulo) es igual, a la suma de los cuadrados de las longitudes de los dos catetos (los dos lados menores del triángulo rectángulo: los que conforman el ángulo recto). Si un triángulo rectángulo tiene catetos de longitudes y , y la medida de la hipotenusa es , se establece que:

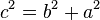
Una circunferencia es un conjunto de puntos del plano equiditantes de otro fijo, llamado centro; esta distancia se denomina radio. Sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perimetro del círculo cuya superficie contiene.

Puede ser considerada como una elipse de ecxentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilindrica, o como un poligono de infinitos lados, cuya apotema coincide con su radio.

La circunferencia de centro en el origen de coordenadas y radio 1 se denominacircunferencia unidad

Es una curva plana con infinitos ejes de simetría y sus aplicaciones son muy numerosas.

El centro es el punto del que equidistan todos los puntos de la circunferencia.

el radio de una circunferencia es el lugar geométrico de los puntos del plano que equidistan de otro punto llamado centro; o también se puede definir como: cualquier recta punto o segmento que va desde su centro a cualquier punto de la circunferencia.

Rango de una función
	El conjunto de todos los valores de salida de una función. Dominio -> función -> Rango Ejemplo: si a la función f(x) = x2 se le dan los valores x = {1,2,3,...} entonces el rango será {1,4,9,...}

El dominio de una función está formado por aquellos valores de x (números reales) para los que se puede calcular la imagen f(x).

Ejemplos:

La recta secante es una recta que corta a unacircunferencia en dos puntos. Conforme estos puntos de corte se acercan, dicha recta se aproxima a un punto y, cuando solo existe un punto que toca la circunferencia, se le llama tangente. "Secante" proviene del término en latín para el verbo cortar => "secare"

Dados los puntos de intersección A y B puede calcularse la ecuación de la recta secante empleando para saber la respuesta de ésta operación se emplea en matemáticas la ecuación de la recta que pasa por dos puntos:

una recta tangente es aquella que solo tiene un punto en común con una curva, es decir la toca en un solo punto, que se llama punto de tangencia. La recta tangente indica la pendiente de la curva en el punto de tangencia.

parabola

La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.

Elementos de la parábola

Foco

Es el punto fijo F.

Directriz

Es la recta fija d.

Parámetro

Es la distancia del foco a la directriz, se designa por la letra p.

Eje

Es la recta perpendicular a la directriz que pasa por el foco.

Vértice

Es el punto de intersección de la parábola con su eje.

Radio vector

Es un segmento que une un punto cualquiera de la parábola con el foco.

función cuadrática o función de segundo grado es una función polinómica que se define mediante un polinomio de segundo grado como:
Gráficas de funciones cuadráticas.

f(x) = ax^2 + bx + c \,

donde a, b y c son constantes y a es distinto de 0.

La representación gráfica en el plano XY haciendo:

y = f(x) \,

esto es:

y = ax^2 + bx + c \,

es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.

FUNCIONES TRIGONOMETRICAS

Una función trigonométrica, también llamada circular, es aquella que se define por la aplicación de una razón trigonométrica a los distintos valores de la variable independiente, que ha de estar expresada en radianes. Existen seis clases de funciones trigonométricas: seno y su inversa, la cosecante; coseno y su inversa, la secante; y tangente y su inversa, la cotangente. Para cada una de ellas pueden también definirse funciones circulares inversas: arco seno, arco coseno, etcétera.
La función seno

Se denomina función seno, y se denota por f (x) 5 sen x, a la aplicación de la razón trigonométrica seno a una variable independiente x expresada en radianes. La función seno es periódica, acotada y continua, y su dominio de definición es el conjunto de todos los números reales.

Gráfica de la función seno.

La función cosecante puede calcularse como la inversa de la función seno expresada en radianes.
La función coseno

La función coseno, que se denota por f (x) = cos x, es la que resulta de aplicar la razón trigonométrica coseno a una variable independiente x expresada en radianes. Esta función es periódica, acotada y continua, y existe para todo el conjunto de los números reales.

Gráfica de la función coseno.

La función secante se determina como la inversa de la función coseno para un ángulo dado expresado en radianes.
La función tangente

Se define función tangente de una variable numérica real a la que resulta de aplicar la razón trigonométrica tangente a los distintos valores de dicha variable. Esta función se expresa genéricamente como f (x) = tg x, siendo x la variable independiente expresada en radianes.

Gráfica de la función tangente.

La función cotangente es la inversa de la tangente, para cualquier ángulo indicado en radianes.