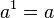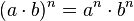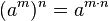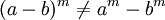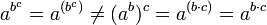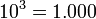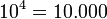en esta tercera semana aprendi varias cosas sobre matemaricas por ejemplo:
las propiedades de la potenciacion

Propiedades de la potenciación ]

Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:

Potencia de exponente 0

Cualquier número $a \in\mathbb{R}\,$ elevado a 0, distinto de 0, es igual a 1

$a^0 = 1\,$

El caso especial $00$ se considera indefinido y dependiendo del contexto pueden ser asignados distintos valores dependiendo de las propiedades específicas que se quieran mantener.

Por ejemplo, puede argumentarse que $00$ es el igual al valor del límite

$\lim_{x\to 0^+} x^0$

y como $x 0 = 1$ para 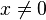$x \ne 0$ , dicho valor podría ser igual a 1. Sin embargo también puede considerarse dicha expresión como el valor del límite

$\lim_{x\to 0^+} 0^x$

y como $0 x = 0$ para 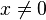$x \ne 0$ , dicho valor podría ser igual a 0. Esto ilustra que la forma $00$ puede corresponde a diferentes valores y por ello se considera indefinida.

El debate sobre el valor de la forma $00$ tiene casi 2 siglos de antigüedad. Durante los primeros días del análisis matemático en que el fundamento formal del cálculo no se había establecido, era común aceptar que 0⁰=1. Sin embargo, en 1821 cuando Cauchy publica el Cours d'Analyse de l'École Royale Polytechnique estableciendo el primer tratamiento riguroso del análisis, lista dicha forma en una tabla de formas indefinidas junto a otras como 0/0. En los 1830s, Libri^[1] ^[2] publicó un argumento para asignar 1 como valor de 0⁰ y August Möbius^[3] lo apoyó afirmando erróneamente que

$\lim_{t \to 0^+} f(t)^{g(t)} = 1\,$ siempre que $\lim_{t \to 0^+} f(t) = \lim_{t \to 0^+} g(t) = 0.$

Sin embargo un comentarista que firmó simplemente como «S» proporcionó un contraejemplo

${(e^{-1/t})}^t$

cuyo límite cuando 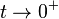$t\to0^+$ es $1 / e$ , lo cual calmó el debate con la aparente conclusión del incidente que 0⁰ debería permanecer indefinida. Se pueden encontrar más detalles en Knuth (1992).^[4]

En la actualidad, suele considerarse la forma $00$ como indefinida y no se le asigna valor si no se tiene un contexto en el cual el valor asignado tenga sentido. ^[5] ^[6] ^[7]

Para calcular límites cuyo valor aparente es $00$ suele usarse la Regla de L'Hopital.

Potencia de exponente 1

Toda potencia de exponente 1 es igual a la base.

$a^1 = a \,$

ejemplo:

$54^1=54 \,$

Multiplicacion de potencias de igual base

El producto de dos o más potencias de igual base «a» es igual a la potencia de dicha base «a» y exponente igual a la suma de los correspondientes exponentes (la misma base y se suman los exponentes):

$a^m \cdot a^n = a^{m + n}$

ejemplos:

$9^3 \cdot 9^2 = 9^{3+2}= 9^5$

Division de Potencias de Igual Base [editar]

La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos (la misma base y se restan los exponentes):

$\frac{a^m}{a^n}=a^{m - n}$

Potencia de un producto

La potencia de un producto es igual a cada uno de los factores del producto elevados al exponente de dicha potencia. Es decir, una potencia de base (a.b) y de exponente "n", es igual al factor "a" elevado a "n" por el factor "b" elevado a "n".

$(a \cdot b)^n=a^n \cdot b^n$

Potencia de una potencia

La potencia de una potencia de base a es igual a la potencia de base a elevada a la multiplicación de ambos exponentes (la misma base y se multiplican los exponentes):

$(a^m)^n = a^{m \cdot n}$

Propiedad distributiva

La potenciación es distributiva con respecto a la multiplicación y a la división:

$(a \cdot b)^n = a^n \cdot b^n$

$\Big(\frac{a}{b}\Big)^n = \frac{a^n}{b^n}$

pero no lo es con respecto a la suma ni a la resta.

Propiedades que no cumple la potenciación

No es distributiva con respecto a la adición y sustracción:

$(a + b)^m \neq a^m + b^m$

$(a - b)^m \neq a^m - b^m$

No cumple la propiedad conmutativa, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes.

En general:

$a^b \neq b^a$

Tampoco se cumple la propiedad asociativa:

$a^{b^c}=a^{(b^c)}\ne (a^b)^c=a^{(b\cdot c)}=a^{b\cdot c}$

Potencia de base 10

En las potencias con base 10, el resultado será la unidad seguida de tantos ceros como indica la cifra del exponente.

Ejemplos:

$10^2=100 \,$

$10^3=1.000 \,$

$10^4=10.000 \,$

$10^5=100.000 \,$

Potencia de números complejos

Para cualquiera de los números reales $a,b,c,d \,$ se tiene la identidad:

$\left(a\,e^{i\,b}\right)^{\left(c\,e^{i\,d}\right)}=a^{c\,\cos d}\,e^{i\,\left( c\,\log a\,\sin d+b\,c\,\cos d\right)-b\,c\,\sin d}$
TAMBIEN APRENDI SOBRE LAS PROPIEDADES DE LA RADICACION

Propiedades de la radicación

Las propiedades de la radicación son bastante similares a las propiedades de la potenciación, puesto que una raíz es una potencia con exponente racional.

Ejemplo:

$\sqrt[4]{x^3}$ = $\ x^{3/4}$ .

Raíz de un producto [editar]

La raíz cuadrada de un producto A x B es igual al producto de la raíz cuadrada de "A" por la raíz cuadrada de "B"

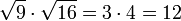
$\sqrt{3^2 \cdot 2^4}$ = $\sqrt{9} \cdot \sqrt{16} = 3\cdot 4 = 12$

Y si se multiplica z x dentro del radical, el resultado será el mismo:

$\sqrt{3^2 \cdot 2^4} = \sqrt{9 \cdot 16} = \sqrt{144} = 12$

Raíz de un cociente [editar]

El cociente de la raíz de una fracción, es igual al cociente de la raíz del numerador entre la raíz del denominador....

$\sqrt[n]{\frac{a}{b}} = \frac{a^{1/n}}{b^{1/n}}$ = $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

Ejemplo:

$\sqrt{\frac{9}{4}} = \frac{\sqrt{9}}{\sqrt{4}}$ = $\frac{3}{2}$

Cuando esta propiedad se hace con números no hace falta pasar la raíz a potencia de exponente racional, aunque sí cuando se hace con variables.

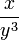
$\sqrt[3]{\frac{x^3}{y^9}} = \frac{x^{3/3}}{y^{9/3}}$ = $\frac{x}{y^3}$

Ejemplo:

$(\sqrt[4]{a^2})^8 = (\ a^{2/4})^8$ = $\sqrt[4]{a^{16}}$

Raíz de una raíz [editar]

Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical.

$\sqrt[n]{\sqrt[m]{a}}$ = $\sqrt[n.m]{a}$

Ejemplo:

$\sqrt[7]{\sqrt[3]{5}}$ = $\sqrt[21]{5}$

POR SUPUESTO ESTA SEMANA APRENDI MUCHO DE DESIGUALDADES PRINCIPALMENTE DE LAS INECUACIONES LINEALES .

EJEMPLO:

3x-5>x+7= 3x-x>7+5
2x>12
x>6

Regla de divisibilidad por 2

Observa los múltiplos de 2:
4; 6; 8, 10; 12; 14; 16; 18; 20; 22; 24; 26; 28;...
Recuerda lo fácil que fue eliminar los múltiplos de 2 en la Criba de Eratóstenes. ¿Por qué era tan fácil? ¿Qué tienen en común todos los múltiplos de 2? ¿En qué acaba todo múltiplo de 2?

Divisibilidad por 4

Un número es divisible por 4 si el número formado por sus dos últimas cifras es divisible por 4.

Por ejemplo, 45,253. Toma las dos últimas cifras: 53. 53 no es divisible por 4, y tampoco es 45,253.

Otro ejemplo: ya que 80 es divisible por 4, entonces 3280, 32480, 293180 etcetera todos son divisibles por 4.

Divisibilidad por 5

Es muy facil: si la última cifra de un núm

Divisibilidad por 6

Si un número es divisible tanto por 2 como por 3, es divisible por 6.

Regla de divisibilidad por 7

Esto es mucho más difícil.
Para saber si un determinado número es divisible por 7 pues hacemos la división y observamos si el resto es cero...
Que es cero.... El número es divisible por 7
Que no lo es... El número no es divisible por 7 Smiling emoticon

Esto evidentemente, no es ninguna regla, es el concepto inicial de divisibilidad aplicable a cualquier primo o no primo...
Pero hay una regla muy curiosa que no todo el mundo conoce. Te la explico:
Paso 1.- Eliminas la cifra de las unidades del número.
Paso 2.- Al número que queda, le restas el doble de la cifra eliminada.
Paso 3.- Repites los pasos 1 y 2 hasta que llegues a un número de una cifra o de dos pero que la cifra de las decenas sea menor que el doble de la cifra de las unidades...
Y observas el resultado: Si el número final es cero, siete u otro múltiplo de 7, es que el número es divisible.
En caso de que no salga un múltiplo de 7, el número no es divisible por 7.
Pongamos un ejemplo:
¿Es 1652 divisible por 7?
Paso 1.- Eliminamos la cifra de las unidades. El número que queda es el 165
Paso 2.- Al 165 le restamos el doble de 2, es decir, 4:
165 - 4 = 161
Repetimos el paso 1.- Eliminamos la cifra de las unidades. El 1. El número que queda es 16
Repetimos el paso 2.- A 16 le restamos el doble de 1, es decir, 2:
16 - 2 = 14
Como 14 es un múltiplo de 7, el número inicial, el 1652 es divisible por 7

Otro ejemplo:
Ejemplo de la regla de divisibilidad del 7

Ejemplo de la regla de divisibilidad del 7

asuntos de matematicas

jueves, 18 de febrero de 2010

viernes, 5 de febrero de 2010

tercera semana de estudio

Propiedades de la potenciación ]

Potencia de exponente 0

Potencia de exponente 1

Multiplicacion de potencias de igual base

Division de Potencias de Igual Base [editar]

Potencia de un producto

Potencia de una potencia

Propiedad distributiva

Propiedades que no cumple la potenciación

Potencia de base 10

Potencia de números complejos

Propiedades de la radicación

Raíz de un producto [editar]

Raíz de un cociente [editar]

Raíz de una raíz [editar]

jueves, 4 de febrero de 2010

criterios de divisibilidad

Regla de divisibilidad por 2

Regla de divisibilidad por 7

Seguidores

Archivo del blog

Datos personales